LA COSTANTE DI AVOGADRO
Settembre 18, 2024In questo articolo viene indicato uno dei metodi per ottenere la costante di Avogadro. Il passaggio dalla denominazione numero di Avogadro a costante di Avogadro è avvenuto nel 1971 quando la mole fu introdotta come grandezza indipendente dalle altre sei fondamentali. Conseguentemente la costante di Avogadro ha assunto come unità di misura mol−1.
Perchè l’allievo possa comprendere il metodo è necessario che conosca :
1- la densità
d= massa/volume) ; Volume = massa/densità massa = densità x volume
2- le unità di misura della lunghezza a livello atomico
Angstrom = 10-8 cm
Nanometri =nm= 10-9 cm
picometri = 10-10 cm
1A= 100 picom = 10 nm
CALCOLO DELLA COSTANTE DI AVOGADRO
La costante di Avogadro rappresenta la costante di proporzionalità vigente tra il numero di entità di un campione e la sua quantità di sostanza, infatti è definita matematicamente come
NA = numero di entità(cioè moli ,atomi o elettroni)/la quantità di sostanza dello stesso campione
Andremo quindi a calcolare il valore di NA da dati cristallografici.
Avogadro ipotizzò che volumi uguali di gas anche se differenti ma che si trovano nelle stesse condizioni di Temperatura e Pressione, contengono un ugual numero di molecole.
Si può facilmente dedurre che se per due gas il numero di molecole N1 è uguale al numero di molecole N2 è evidente che il peso dei due gas deve essere diverso.
Se indichiamo con N il numero di molecole contenute in una quantità di composto gassoso pari al suo peso molecolare sarà anche N il numero di atomi presenti in una quantità pari al peso atomico di un qualunque metallo. Questo ci permette di calcolare N dallo studio dei metalli.
CHE STRUTTURA HA UN METALLO ?
Se frantumiamo idealmente un pezzetto di metallo sino a raggiungere una dimensione così piccola da non poter essere più frantumato e se potessimo osservare il metallo in queste condizioni, con un microscopio potentissimo, vedremmo che il metallo è costituito da unità geometriche uguali (cubo,ottaedro ecc.) che si ripetono una accanto all’altra e nelle 3 dimensioni. Questa unità geometrica si chiama “CELLA UNITARIA” o CELLA ELEMENTARE.
La forma più semplice di una cella elementare di un metallo è il cubo .

in ogni vertice cubo vi è 1 atomo quindi in ogni cubo vi sono 8 atomi. Ogni cubo è circondato da altri cubi per cui possiamo notare che la struttura è la seguente.
Questa struttura è costituita da 8 cubi. Se consideriamo l’atomo al centro degli 8 cubi notiamo che è condiviso da 8 cubi quindi appartiene solo per 1 / 8 ad un solo cubo. Quindi se 1 atomo è condiviso da 8 cubi e se ogni cella elementare unitaria (1 cubo) vi sono 8 atomi ai vertici, in questa cella elementare poichè ogni atomo contribuisce per 1/8 alla cella unitaria vi sono
8 x 1/8 = 1 atomo.
IN OGNI CELLA ELEMENTARE VI E’ 1 SOLO ATOMO!!!
PERCHE’ OGNI ATOMO (E VE NE SONO 8) AL VERTICE DEL SINGOLO CUBO CONTRIBUISCE ALLA STRUTTURA DI 1 CUBO SOLO PER 1/8 ESSENDO CONDIVISO DA ALTRI 8 CUBI !!
CONSIDERIAMO UNA CELLA UNITARIA DIVERSA DAL SEMPLICE CUBO CHE DIFFERISCE DA QUESTO PER LA PRESENZA DI UN ULTERIORE ATOMO AL CENTRO DI OGNI FACCIA DEL CUBO.
LA CELLA UNITARIA E’ DETTA RETICOLO CUBICO A FACCE CENTRATE
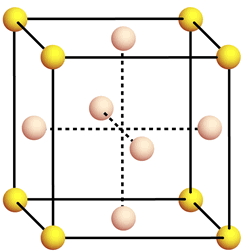
oltre agli 8 atomi ai vertici vi è un atomo al centro di ogni faccia.
OGNI ATOMO AL CENTRO DI UNA FACCIA APPARTIENE A DUE CUBI PER CUI CONTRIBUISCE SOLO PER 1/2 AL SINGOLO CUBO.
ESSENDO 6 LE FACCE DI OGNI CUBO IL NUMERO DI ATOMI DELLE FACCE DI UN SINGOLO CUBO E’
1/2 X 6 = 3 ATOMI
QUESTI SI AGGIUNGONO AGLI ALTRI 1/8 X 8 ATOMI CHE STANNO AI VERTICI (QUINDI 1 ATOMO) ED IN DEFINITIVA
IN UN RETICOLO CUBICO A FACCE CENTRATE SI HANNO
3 + 1 = 4 ATOMI
CONSIDERIAMO ADESSO UN’ALTRA STRUTTURA DI UN CUBO CON UN ATOMO AL CENTRO DEL CUBO
( RETICOLO CUBICO A CORPO CENTRATO)

IN UNA STRUTTURA DI QUESTO TIPO IL NUMERO DI ATOMI E’ 1/8 X 8 =1 (CONTRIBUTO DEGLI ATOMI AL VERTICE) E 1 AL CENTRO QUINDI IL NUMERO TOTALE DI ATOMI E’ 1+1 =2 ATOMI.
RIASSUMENDO
RETICOLO SEMPLICE …………………… 1 ATOMO
RETICOLO A CORPO CENTRATO………. 2 ATOMI
RETICOLO A FACCE CENTRATE ………. 4 ATOMI
CALCOLO DELLA COSTANTE DI AVOGADRO
Consideriamo il reticolo dell’ORO Au esso è un reticolo a facce centrate per cui ogni reticolo ha 4 atomi di oro.
Conoscendo la sua densità che è 19,3 g/ml e conoscendo il peso atomico che è PM= 197 u ( unità di massa atomica unificata) calcoliamo il peso di una cella unitaria dell’oro da d=193 /V
ma V= l3
l (il lato) può essere calcolato dal metodo di Bragg che trovò che le sostanze cristalline producevano spettri di diffrazione caratteristici. Bragg interpretò questo fatto sperimentale considerando i cristalli come costituiti da una successione di piani paralleli di ioni, distanziati di una lunghezza d (ovvero una successione di piani del reticolo).
2d sinθ = n λ
è stato calcolato che per l’oro d= l=407,7 x 10 -10 cm pertanto l3 = (407,7 x 10 -10 )3 = 6,776 x 10-30 cm
conoscendo il volume si può calcolare la massa della cella unitaria dal valore della densità
m= 19,3 x 6,7776 x 10-30 = 130,85 x 10-23
Poichè in una cella unitaria di oro vi sono 4 atomi per conoscere quanti atomi vi sono in una quantità di oro pari al Patomico (197 g) è sufficiente la proporzione :
se in 130.85 x 10-23 :4 atomi =in 197 :X X= 197 x 4 /130.85 x 10-23
X= 6,022 x 1023 atomi
se ripetiamo il calcolo per atomi diversi con strutture anche diverse seguendo lo stesso metodo troveremo sempre che in una quantità pari al peso atomico di qualsiasi atomo metallico vi sono 6,022 x 1023 atomi
6,022 x 1023 atomi è la costante di Avogadro

